A Brief Exploration of a Möbius Transformation
As part of a recent homework set in my complex analysis course, I was tasked with a problem that required a slight generalization on part of Schwarz’s Lemma:
Lemma (Schwarz): Let $f$ be analytic on the unit disk with $|f(z)| \leq 1$ for all $z$ on the disk and $f(0) = 0$. Then $|f(z)| < |z|$ and $f’(0)\leq 1$.
If either $|f(z)|=|z|$ for some $z\neq0$ or if $|f’(0)|=1$, then $f$ is a rotation, i.e., $f(z)=az$ for some complex constant $a$ with $|a|=1$.
The homework assignment asked us (within the context of a larger problem) to consider the case when $f(\zeta) = 0$ for some $\zeta \neq 0$ on the interior of the unit disk. The secret to this problem was to find some analytic function $\varphi$ that maps the unit disk to itself, but swaps $0$ and $\zeta$. Then, we may consider $\varphi^{-1}\circ f\circ \varphi$ and apply Schwarz’s Lemma.
Properties of the transformation
The appropriate map, which is a particular Möbius transformation, is given by the following:
$$\varphi_\zeta(z) = \frac{\zeta - z}{1-\overline{\zeta}z}$$
Now, if $|z| = 1$, then $|\varphi_\zeta(z)| = |\overline{z} \varphi_\zeta(z)| = \left|\frac{\overline{z}\zeta-1}{1-\overline{\zeta}z}\right| = 1$. Therefore, this map takes the boundary of the unit disk to itself.
Further, this $\varphi_\zeta$ is analytic within the unit disk, as its only singularity occurs when $|z| > 1$ (since this occurs when $z = \frac{1}{\overline{\zeta}}$ and $\left|\overline{\zeta}\right| < 1$). And, finally, since $\varphi_\zeta$ is non-constant, the maximum modulus principle tells us that $|\varphi_\zeta(z)| < 1$ when $|z| < 1$.
Therefore, $\varphi_\zeta$ maps the unit disk onto itself, where $\varphi_\zeta(\zeta) = 0$ and $\varphi_\zeta(0) = \zeta$.
Another useful feature of this map is that it is an involution. That is, $\varphi_\zeta^{-1} = \varphi_\zeta$. An application of Schwarz’s Lemma shows this immediately: since $\varphi\circ\varphi$ fixes two points in the unit disk (one of them zero) and satisfies the modulus bound, we can conclude that $\varphi\circ\varphi$ is the identity. Therefore, $\varphi$ is its own inverse.
Impact of this map on the unit disk
I was curious what this mapping does to the values on the unit disk. We’ve clearly swapped $\zeta$ and $0$, but the map must maintain analyticity on the unit disk, so it must do more than just that. I wanted to know how this distortion affects the rest of the values on the disk. So, I wrote a quick Python program to generate a couple of plots:
1import numpy as np
2import matplotlib.pyplot as plt
3
4from math import pi
5from cmath import phase as arg
6
7# Create a 2D grid on which to evaluate the function
8xs = np.linspace(-1, 1, num = 700)
9ys = np.linspace(-1, 1, num = 700)
10X, Y = np.meshgrid(xs, ys)
11
12# Round it off to be only the unit circle
13r = np.sqrt(X**2 + Y**2)
14X = np.ma.masked_where(r > 1, X)
15Y = np.ma.masked_where(r > 1, Y)
16
17# The new "zeta" value
18zeta = 0.2 + 0.38j
19
20# The involution, phi
21@np.vectorize
22def phi(z):
23 return (zeta - z) / (1-zeta.conjugate()*z)
24
25vabs = np.vectorize(abs)
26varg = np.vectorize(arg)
27
28# Determine the argument and modulus of points on the unit circle
29Z = X+Y*1.0j
30
31F1 = vabs(phi(Z))
32F2 = vabs(Z)
33F3 = varg(phi(Z))
34F4 = varg(Z)
35
36# Plot them all!
37F = [F1, F2, F3, F4]
38fig, axes = plt.subplots(2, 2)
39titles = [
40 '|$\\varphi_\\zeta(z)$|',
41 '|$z$|',
42 'Arg$(\\varphi_\\zeta(z))$',
43 'Arg$(z)$',
44]
45
46t = np.linspace(0, 2*pi, 100)
47
48for i, ax in enumerate(np.reshape(axes, (-1,))):
49 # draw the heatmap
50 ax.pcolormesh(X, Y, F[i])
51
52 # draw bounding circle
53 ax.plot(np.cos(t), np.sin(t), linewidth=2, color='black')
54
55 # adjust the axis labels
56 ax.set_aspect('equal')
57 ax.set_xlim(-1.1, 1.1)
58 ax.set_ylim(-1.1, 1.1)
59 ax.set_title(titles[i])
60
61plt.tight_layout() # helps with spacing
62plt.show()
Below, we’ve plotted the magnitude and argument (angle) of $z$ and $\varphi_\zeta(z)$ side-by-side. We can now see that, in terms of magnitude, it’s just as if the map “shifted” over the origin, squeezing and pulling the surrounding values to maintain analyticity. However, it also twisted and reflected the values of $z$ on each circle around the origin. (This can be seen through the curve of the $\mathrm{Arg}(\varphi_\zeta(z))$ plot.)
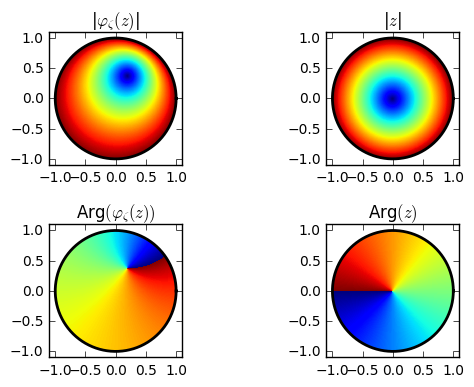
Resulting plots
Conclusion
This doesn’t really serve much purpose in and of itself, but it helped build my intuition of what is happening when I apply the function $\varphi$ and developed my abilities in numpy and matplotlib usage. The Schwarz Lemma is an interesting topic in Complex Analysis, and I based some of my initial work on a 2010 paper by Dr. Harold P. Boas, entitled Julius and Julia: Mastering the art of the Schwarz lemma. Of particular note is “Section 3: Change of Base Point,” where he develops and discusses the map $\varphi$.