Many computer science problems utilize graph-based data structures. Their use can range from explicit inclusion in an algorithm-centric problem (like path-finding) to a more “behind-the-scenes” presence in Bayesian networks or descriptions of finite automata. Unfortunately, visualizing large graphs can be difficult to do, especially for debugging. Unlike lists or dictionaries, which can be represented clearly by plain text printing, depicting a graph tends to require more graphics overhead than is reasonable for most programmers to write simply for debugging purposes. I’ve found that Graphviz, a free graph visualization utility, can be quite useful in debugging graph-related programs.

Installing Graphviz

If you’re on a Debian-based Linux OS (e.g. Ubuntu), you can install Graphviz using apt-get. Just run $ sudo apt-get install graphviz and you’ll have everything you need to complete the steps in this blog post. Mac OS X users can use brew equivalently.

Windows users should install using a binary downloaded from the Graphviz Windows page, but there might be some issues with setting the PATH variable for running in the commandline.

Making a basic graph

Once you’ve installed, the next thing you’ll want to do is create a basic graph to ensure the installation succeeded and to gain practice using Graphviz tools. We do this by creating a *.dot file that describes the graph we wish to display. If you’re the type of person who likes to jump right in and experiment first before reading too much, or if you love formal language specification, the DOT grammar is fairly readable and can give a quick introduction to creating DOT files.

The below is a fairly representative DOT file to demonstrate some of the capabilities of Graphviz. Open your favorite text editor, copy/paste it in, and save it as firstgraph.dot:

 1digraph G {
 2  // Style information for nodes
 3  A [style="filled", color=".05 .3 1.0"]
 4
 5  // Edge declarations
 6  A -> {B, C};
 7  D -> E [label="-1"];
 8  E -> F [label="3"];
 9  F -> D [label="10"];
10}  

This creates a directed graph (also called a digraph) with six nodes and two connected components. Some of the edges have labels, and one of the nodes is colored. After you’ve copied (or downloaded) this file, open up a terminal to the directory with firstgraph.dot in it and run $ dot firstgraph.dot -Tpng -o firstgraph.png. The resulting image file should look something like the below:

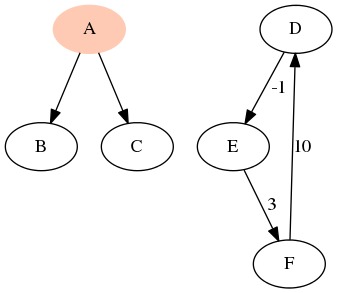
The rendered `firstgraph.dot`

This past week, my ICPC team worked the 2013 Greater New York Regional problem packet. One of my favorite problems in this set was Problem E: Deranged Exams. The code required to solve this problem isn’t that complicated, but the math behind it is a little unusual. In this post, I aim to explain the math and provide a solution to this problem.

Problem Description

The full problem statement is archived online; in shortened form, we can consider the problem to be:

Given a “matching” test of $n$ questions (each question maps to exactly one answer, and no two questions have the same answer), how many possible ways are there to answer at least the first $k$ questions wrong?

It turns out that there’s a really nice solution to this problem using a topic from combinatorics called “derangements.” (Note that the problem title was a not-so-subtle hint towards the solution.)

Derangements

While the idea of a permutation should be familiar to most readers, the closely related topic of a derangement is rarely discussed in most undergraduate curriculum. So, it is reasonable to start with a definition:

A derangement is a permutation in which no element is in its original place. The number of derangements on $n$ elements is denoted $D_n$; this is also called the subfactorial of $n$, denoted $!n$.

The sequence $\langle D_n\rangle$ is A000166 in OEIS (a website with which, by the way, every competitive programmer should familiarize themselves).

It turns out that there is both a recursive and an explicit formula for $D_n$:

{% math %} \begin{aligned} D_n &= (-1)^n \sum_k\binom{n}{k} (-1)^k k! \ &= n\cdot D_{n-1} + (-1)^n;;(D_0=1) \end{aligned} {% endmath %}

This is significant because we can use the explicit formulation for computing single values of derangements, or we can use dynamic programming to rapidly compute $D_n$ for relatively small $n$.

A friend recently emailed me asking for titles of books I’d recommend to read over the summer, particularly to prepare for computer science and mathematics. I’ve adapted my suggestions into this post. I’d like to note that I’ve restricted my responses to “non-textbooks;” otherwise, I’d have several more additions that would increase the average page count and price quite drastically. As such, these books don’t have problems to work or present an extreme level of detail, but in many cases they present enough information to provide a strong foundation and context for math and CS classes.

From Mathematics to Generic Programming

Alexander Stepanov and Daniel Rose (on Amazon)

I will most likely write a separate blog post about this book. I read it during the end of the fall semester and found that it presented a very interesting approach to designing reusable code by utilizing principles from abstract algebra. It’s written to be accessible by someone who hasn’t studied abstract algebra yet, which means it also can serve as an introduction to that subject.

CODE: The Hidden Language of Computer Hardware and Software

Charles Petzold (on Amazon)

Four years ago, I wrote a review of this book on RoboDesigners. At that time, my perspective was that of a high school student and I thought the book was interesting; with the additional perspective of a year of college study in Computer Science, I cannot recommend this book highly enough.

By “building” a computer piece-by-piece from the idea of a relay through developing a simple assembly language, it covers nearly all of the material as the Digital Logic Design course I took, but in an easy-to-read book. If you comprehend the material in this book, you will be able to coast through DLD.

A Mathematician’s Apology

G. H. Hardy (on Amazon)

When a mathematician with Hardy’s stature writes a book on why he studies math, it’s probably advisable to read it! Multiple professors of mine have said it’s a book any mathematician should read and I wholeheartedly agree. It’s really short (the printing I’ve linked above is only 154 pages), but the content is amazing. Hardy addresses the complaints many have with pure math and embodies the spirit of “doing mathematics for mathematics’ sake.” If you are thinking about pursuing a theoretical route in either CS or math, I highly recommend you read this book.

How many divisors are there of the number $1281942112$? It turns out that determining the answer to this problem is (at most) only as difficult as determining the prime factorization of the number. In this blog post, I will outline a solution to this (and similar) problems.

The Math

The Fundamental Theorem of Arithmetic guarantees each positive integer greater than $1$ a unique prime factorization. We write this factorization as:

$$N = p_0^{e_0}p_1^{e_1}\cdots p_n^{e_n}$$

where $p_k$ is a prime number, and $e_k$ is its corresponding exponent. This provides us with useful information regarding divisors of $N$: any divisor of $N$ must be comprised of some combination of those prime factors (and exponents). Specifically, we can define the divisor, $D$, as:

$$D = p_0^{a_0}p_1^{a_1}\cdots p_n^{a_n}$$

where the $p_k$ are the same as in the factorization of $N$ and $a_k \in {0, 1, \ldots, e_k}$. To find the total number of divisors, we multiply together the number of options we have for each exponent. That is,

$$\text{Number of Divisors}; = (e_0+1)(e_1+1)\cdots(e_n + 1)$$

Example: Consider $N = 20$. In this case, $N$ has $6$ divisors; to determine this without needing to list them all, we may note that $N = 2^2\cdot 5^1$. Using the notation described above, this means that $p_0 = 2,;p_1 = 5$ and $e_0 = 2;e_1 = 1$. Each of our divisors will be of the form $2^{a_0}\cdot 5^{a_1}$, where $a_0$ could be $0, 1,$ or $2$ and $a_1$ could be $0$ or $1$. Since we have $e_0+1 = 3$ options for $a_0$ and $e_1+1 = 2$ options for $a_1$, we have $3\cdot 2 = 6$ total divisors. In case you were wondering, the list of divisors is:

$${2^0 5^0, 2^1 5^0,2^2 5^0,2^0 5^1,2^1 5^1,2^2 5^1}$$